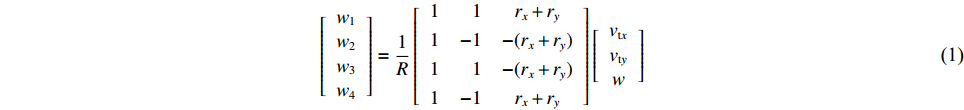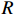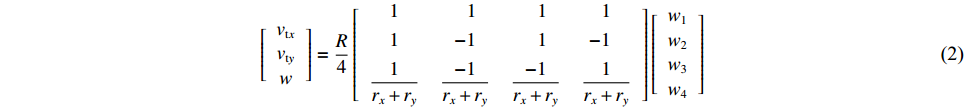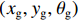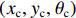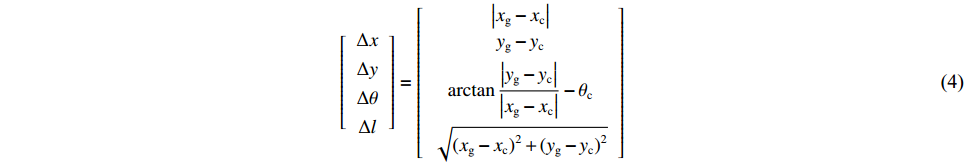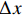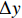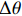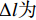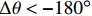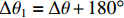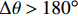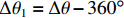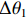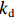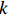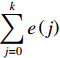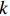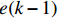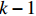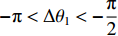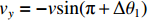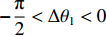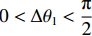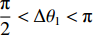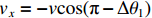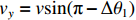Local Path Planning of Indoor Mobile Robot Based on Dijkstra and PID Algorithm
-
摘要:
针对普通轮式机器人在室内难以通过狭小工作区域,易陷入局部区域无法完成导航的问题,提出一种麦克纳姆轮式机器人底盘的局部路径规划融合算法。借鉴麦克纳姆轮的优势,采用Dijkstra全局路径规划算法规划全局路径,融合Dijkstra和PID算法控制局部路径规划;根据姿态信息将机器人速度进行横向和纵向分解,限制旋转速度,在保持姿态不变的前提下驱动机器人实现稳定移动;使用搭载机器人操作系统的麦克纳姆轮式机器人进行导航测试试验,验证本文融合算法的有效性。结果表明:在复杂狭窄的室内环境下,本文算法可实现机器人的自主导航与避障,可成功地从设定的起点到达终点;与传统的时间弹性带(TEB)算法相比,本文算法在无障碍的环境中导航时间减少了30.56%,在有障碍物环境中导航成功率可提高4%,能够满足室内移动机器人快速到达导航目标点的需求。
Abstract:Aiming at the problem that ordinary wheeled robots are difficult to pass through a narrow working area indoors, and are easily trapped in a local area and unable to complete navigation, a local path planning fusion algorithm for Mecanum wheeled robot chassis was proposed. Based on the advantages of the Mecanum wheel, the Dijkstra global path planning algorithm was used to plan the global path, and the Dijkstra and PID algorithms were combined to control the local path planning. According to the attitude information, the robot speed was decomposed laterally and vertically, the rotation speed was limited to drive the robot to achieve stable movement while keeping the attitude unchanged. The Mecanum wheeled robot equipped with the robot operating system was used for navigation test to verify the effectiveness of the fusion algorithm in this paper. The results show that in a complex and narrow indoor environment, the algorithm can achieve autonomous navigation and obstacle avoidance of the robot, and can successfully reach the destination from the set starting point. Compared with the traditional time-elastic band (TEB) algorithm, the navigation time of this algorithm in an obstacle-free environment is reduced by 30.56%, and the navigation success rate in an obstacle environment is 4% higher, which can meet the demand of indoor mobile robots to reach the navigation target point quickly.
-
Keywords:
- robot operating system /
- Mecanum wheel /
- fusion algorithm /
- local path planning
-
新冠疫情的爆发、人口老龄化的加剧给传统服务业带来了巨大的挑战,室内移动机器人作为服务业产业升级和创新发展的标志性产品之一,对服务业的发展发挥重要作用。以麦克纳姆轮为底盘构建的移动机器人移动平台能够在室内二维平面上朝不同方向自由移动,具有其他普通轮式移动平台不可替代的特点,被广泛用于室内不同的场景。因此,在麦克纳姆轮底盘运动学的基础上,如何实现路径规划算法是室内移动机器人发展的一个重要方向。
根据已知的环境信息和规划范围的不同,路径规划分为全局路径规划和局部路径规划[1]。其中:全局路径规划是在已知的环境地图下,机器人进行一次规划得到一条连接起点和终点的无碰撞路径,常用的算法有Dijkstra算法[2]、蚁群算法[3–4]、A*算法[5–6]及改进的JPS算法[7]等;局部路径规划算法有动态窗口法(dynamic window approach,DWA)、时间弹性带(time elastic band,TEB)算法。DWA算法存在部分评价函数权值不足、在复杂环境下导航失败等问题[8];TEB算法作为时间最短的最优控制器,在参数约束下会出现速度和方向的震荡问题[9]。徐保来等[10]提出了适用于阿克曼机器人的改进DWA算法,仿真实验得出改进算法的速度空间能满足阿克曼移动机器人的运动约束,可规划出机器人的运动控制指令,但该算法需调整大量参数,仅集中于理论验证与仿真实验阶段,缺乏真实的机器人平台验证;Zhang 等[11]提出一种在线参数自适应的DWA算法,通过自动调整目标函数的权重来获得移动机器人的合理路径;郑凯林等[12]提出了一种增加加速度约束的改进TEB算法,通过增加轨迹优化过程中的加速度约束实现了轨迹平滑的运动效果,并在真实的机器人平台上得到了应用,但机器人在通过室内狭窄的环境时,需调整大量参数进行减速避障。为解决上述问题,并满足导航精度与鲁棒性的要求,提出一种针对麦克纳姆轮[13]底盘的局部路径规划算法,结合Dijkstra全局路径算法和PID算法进行局部路径规划,以期实现机器人在室内复杂环境中的路径规划与导航。
1. 路径规划融合算法
移动机器人控制系统的核心是路径规划[14–15]。在已知环境地图的前提下,机器人获得目标点后,全局路径规划器就会规划出一条从起点到终点的大致可行路线,该路线即为全局路径,全局路径规划是静态的,不能有效处理环境中的动态障碍物。在实际工作环境中,机器人不可避免地遇到各种障碍物,为确保机器人安全顺利地到达目标点,需要局部路径规划器根据已有的全局路径与实时的环境信息,动态规划出机器人能够安全避障的运动轨迹,随机器人的不断移动实时规划直到终点。
1.1 机器人的运动学分析
文中研究的移动机器人由麦克纳姆轮底盘搭建而成,麦克纳姆轮由轮毂和一组均匀排布在轮毂周围的辊子组成,一般情况下辊子轴线和轮毂轴线夹角成45°。麦克纳姆轮可分为互为镜像关系的A轮和B轮,A轮可斜向左前右后方运动,B轮可斜向右前左后方运动[13]。麦克纳姆轮底盘在室内平坦地面可实现横向或纵向平移的运动,可在不改变朝向的情况下进行全方向移动,不存在最小转弯半径约束的问题,在工作空间有限的环境中也可实现正常运动,具有良好的机动性与灵活性[14]。
假设机器人在运动过程中不会悬空,且不会发生空转现象;同时将机器人视为刚体,刚体在平面上的运动可分解为3个独立分量,则机器人几何中心的速度
$ {v}_{{\rm{t}}} $ 可表示为$ {\left[\begin{array}{ccc}{v}_{{\rm{t}}x}& {v}_{{\rm{t}}y}& w\end{array}\right]}^{\mathrm{T}} $ ,其中vtx,vty为机器人的水平分速度,w为机器人的角速度。令轮子的速度为$ {v}_{1}, {v}_{2},{v}_{3},{v}_{4} $ ;转速为$ {w}_{1},{w}_{2},{w}_{3},{w}_{4} $ ;$ {\boldsymbol{r}} $ 为机器人底盘几何中心指向轮子轴心的向量;$ {v_r} $ 为轮子轴心沿垂直于$ {\boldsymbol{r}} $ 方向的速度分量;${r_x}$ 和${r_y}$ 为$ {\boldsymbol{r}} $ 在几何中心坐标系$ x $ 轴和$ y $ 轴上的投影距离。机器人运动分析如图1。麦克纳姆轮底盘4个轮子的转速可表示为:
$$ \left[ {\begin{array}{*{20}{c}} {{w_1}} \\ {{w_2}} \\ {{w_3}} \\ {{w_4}} \end{array}} \right] = \frac{1}{R}\left[ {\begin{array}{*{20}{c}} 1&\;\;\;1&{{r_x} + {r_y}} \\ 1&{ - 1}&{ - ({r_x} + {r_y})} \\ 1&\;\;\;1&{ - ({r_x} + {r_y})} \\ 1&{ - 1}&{{r_x} + {r_y}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{v_{{\rm{t}}x}}} \\ {{v_{{\rm{t}}y}}} \\ w \end{array}} \right] $$ (1) 式中
$R$ 表示麦克纳姆轮半径,式(1)为机器人平台逆运动学方程。机器人平台正运动学方程可用式(2)表示。$$ \left[ {\begin{array}{*{20}{c}} {{v_{{\rm{t}}x}}} \\ {{v_{{\rm{t}}y}}} \\ w \end{array}} \right] = \frac{R}{4}\left[ {\begin{array}{*{20}{c}} 1&\;\;\;1&\;\;\;1&1 \\ 1&{ - 1}&\;\;\;1&{ - 1\;\;\;} \\ {\dfrac{1}{{{r_x} + {r_y}}}}&{\dfrac{{ - 1}}{{{r_x} + {r_y}}}}&{\dfrac{{ - 1}}{{{r_x} + {r_y}}}}&{\dfrac{1}{{{r_x} + {r_y}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{w_1}} \\ {{w_2}} \\ {{w_3}} \\ {{w_4}} \end{array}} \right] $$ (2) 为使机器人更好地发挥麦克纳姆轮的特性,限制其旋转速度、减少转弯时间、提高运动效率,令
$ w=0 $ ,则底盘4个轮子的转速可简化为式(3):$$ \left[ {\begin{array}{*{20}{c}} {{w_1}} \\ {{w_2}} \\ {{w_3}} \\ {{w_4}} \end{array}} \right] = \frac{1}{R}\left[ {\begin{array}{*{20}{c}} 1&\;\;\;1 \\ 1&{ - 1} \\ 1&\;\;\;1 \\ 1&{ - 1} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{v_{{\rm{t}}x}}} \\ {{v_{{\rm{t}}y}}} \end{array}} \right] $$ (3) 1.2 路径规划融合算法的实现
Dijkstra算法是典型的单源最短路径算法,按照路径长度递增的次序产生最短路径,主要特点是以起始点为中心,按广度优先搜索(breadth first search,BFS)算法向外遍历,直到找出一条所有节点的最短路径为止,这条路径就是对应起点到终点的最短路径[16]。文中采用Dijkstra算法进行全局路径规划,为避免其陷入局部区域无法到达目标,使局部路径规划能够更好地沿着全局路径,提出一种基于麦克纳姆轮式机器人底盘的局部路径规划,通过PID和Dijkstra算法的融合控制机器人运动,实现到目标点时间最短的目标。
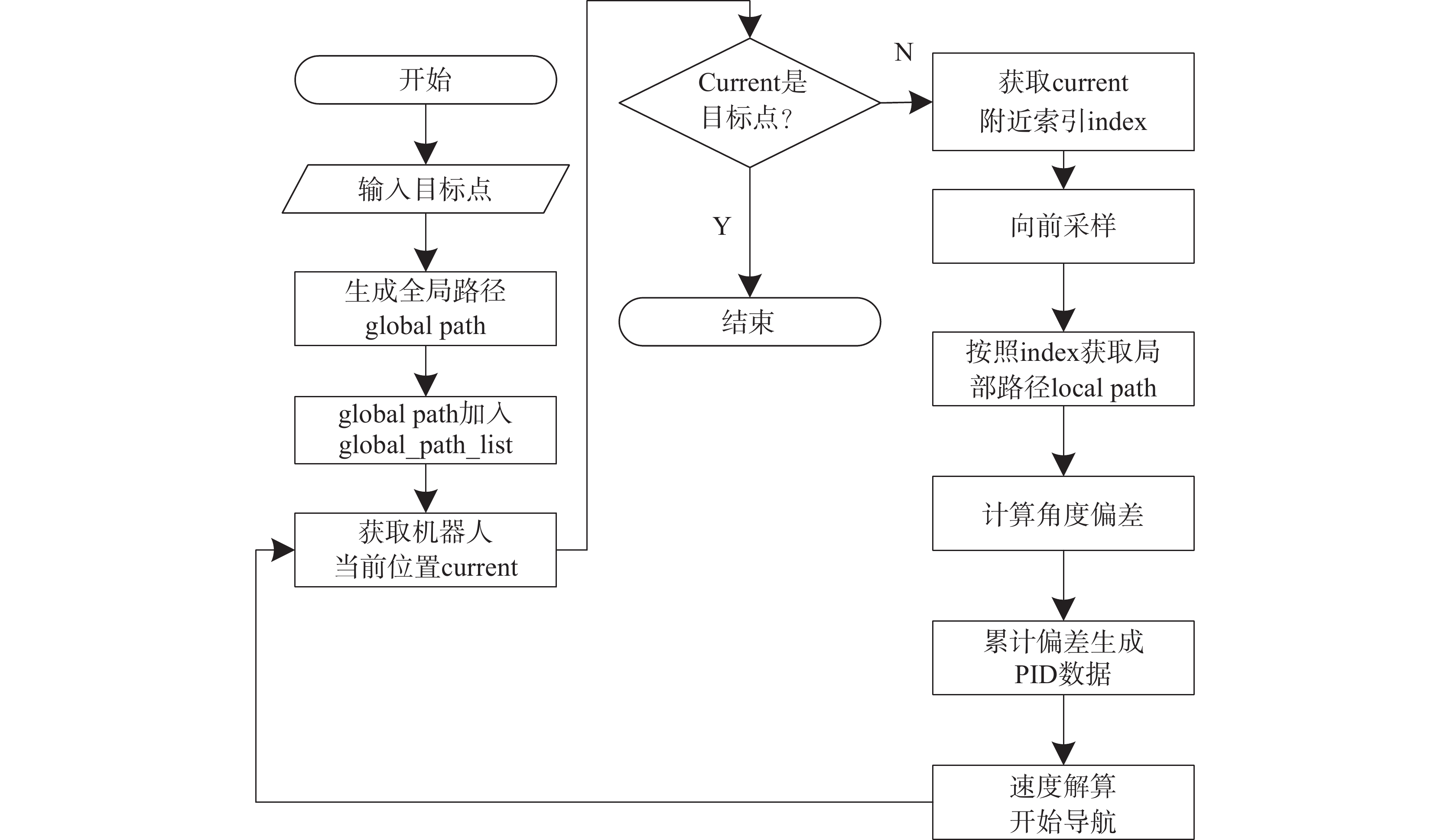
局部路径规划算法流程图如图2。
局部路径规划算法的具体实现过程如下:
1) 全局路径的获取与存储。为能够使机器人顺利从起点到达终点,机器人需获取一条全局路径,在提前建立的栅格地图中给出机器人运动的起点和终点坐标,导航功能包move_base可规划出机器人到目标位置的全局路线,其格式为一组路径点的位姿信息,同时在系统中存储全局路径。
2) 机器人位置的获取。通过里程计信息和激光雷达传感器的测量数据得到机器人在地图坐标系下的位置,由此判断机器人是否到达目标点,便于机器人平稳到达目标区域。
3)局部路径和航向角偏差的获取。从全局路径中获取距离机器人最近的全局路径点作为局部目标起点,按照索引开始采样获取一段路径点,选取该段全局路径,得到初始化轨迹,将其作为机器人移动的局部路径。机器人在进行数据处理和向前运动的过程中有一定的延迟现象,控制器不能实时接收数据。为此,在每次选取全局路径时,都会在局部目标点的基础上向前截取一段路径作为机器人本次的局部路径,然后计算机器人在运动过程中与局部目标点的误差,包括横向偏差、纵向偏差及角度误差。假设在地图坐标系下局部目标点的坐标为
$({x_{{{\rm{g}}}}},{y_{{{\rm{g}}}}},{\theta _{{{\rm{g}}}}})$ ,机器人当前位置的坐标为$({x_{{{\rm{c}}}}},{y_{{{\rm{c}}}}},{\theta _{{{\rm{c}}}}})$ ,则有$$ \left[ {\begin{array}{*{20}{c}} {\Delta x} \\ {\Delta y} \\ {\Delta \theta } \\ {\Delta l} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\left| {{x_{{\rm{g}}}} - {x_{{\rm{c}}}}} \right|} \\ {{y_{{\rm{g}}}} - {y_{{\rm{c}}}}} \\ {\arctan \dfrac{{\left| {{y_{{\rm{g}}}} - {y_{{\rm{c}}}}} \right|}}{{\left| {{x_{{\rm{g}}}} - {x_{{\rm{c}}}}} \right|}} - {\theta _{{\rm{c}}}}} \\ {\sqrt {{{({x_{{\rm{g}}}} - {x_{{\rm{c}}}})}^2} + {{({y_{{\rm{g}}}} - {y_{{\rm{c}}}})}^2}} } \end{array}} \right] $$ (4) 式中:
$ \Delta x $ 为机器人局部目标点与当前位置的纵向偏差绝对值;$ \Delta y $ 为两点间的横向偏差;$ \Delta \theta $ 为航向角偏差,即机器人当前位置与局部目标位置的角度偏差;$ \Delta l\mathrm{为} $ 机器人当前位置与局部目标点之间的距离。根据$ \Delta \theta $ 的大小进行角度校正,若$\Delta \theta < -180{\text{°}}$ ,则$ \Delta {\theta }_{1}=\Delta \theta +180{\text{°}} $ ;若$ \Delta \theta > 180{\text{°}} $ ,则$ \Delta {\theta }_{1}=\Delta \theta -360{\text{°}} $ 。其中$ \Delta {\theta }_{1} $ 为校正后的偏差。4) 局部路径的分析。机器人在导航过程中不断判断前方局部路径的状态,从选取的全局路径中依次取出3个相邻的局部目标点,通过相邻2个局部目标点之间的倾斜角度分析该段局部路径状况,不断累计角度变化值。角度变化较小时,控制器判断前方路径是直线,机器人适当加速;角度变化较大时,控制器判断前方路径进入拐点,即前方有弯道出现,机器人适当减速。随着机器人不断运动,距离终点会越来越近,局部路径数量会不断减少。当局部路径点减少为零,判断机器人到达终点,停止运动,导航结束。
5) PID数据的获取与速度分解。基于上述对局部路径的判断,可确定在不同路况下移动机器人的运动状态,根据当前位置与期望目标位置距离的差值生成对应的机器人合速度,如式(5)。
$$ v = {k_{\rm{p}}} e(k) + {k_{\rm{i}}}\sum\limits_{j = 0}^k {e(j)} + {k_{\rm{d}}}(e(k) - e(k - 1)) $$ (5) 式中:
$ {k}_{{\rm{p}}} $ ,$ {k}_{{\rm{i}}} $ ,$ {k}_{{\rm{d}}} $ 分别为PID的比例、积分、微分系数;期望距离为0,$e(k)$ 表示当前$k$ 时刻机器人距离局部目标点的距离;$\displaystyle\sum\limits_{j=0}^{k}e\left(j\right)$ 为机器人从零时刻到$ k $ 时刻距离局部目标点的累积距离;$ e(k-1) $ 表示$ k-1 $ 时刻距离局部目标点的距离。根据校正后偏差角度将速度分解为横向速度vy和纵向速度vx,定义分解方式如下:若
$-{\text{π}} < \Delta {\theta }_{1} < -\dfrac{{\text{π}} }{2}$ ,则${v}_{x}=-v\mathrm{cos}({\text{π}} +\Delta {\theta }_{1})$ ,${v}_{y}=-v\mathrm{sin}({\text{π}} +\Delta {\theta }_{1})$ ;若
$-\dfrac{{\text{π}} }{2} < \Delta {\theta }_{1} < 0$ ,则${v}_{x}=v\mathrm{cos}\;\Delta {\theta }_{1}$ ,${v}_{y}=-v\mathrm{sin}(-\Delta {\theta }_{1})$ ;若
$0 < \Delta {\theta }_{1} < \dfrac{{\text{π}} }{2}$ ,则${v}_{x}=v\mathrm{cos}\;\Delta {\theta }_{1}$ ,${v}_{y}=v\mathrm{sin}\;\Delta {\theta }_{1}$ ;若
$\dfrac{{\text{π}}}{2} < \Delta {\theta }_{1} < {\text{π}}$ ,则${v}_{x}=-v\mathrm{cos}({\text{π}} -\Delta {\theta }_{1})$ ,${v}_{y}=v\mathrm{sin}({\text{π}} -\Delta {\theta }_{1})$ 。通过以上过程,机器人在得到融合算法的轨迹后,通过校正的角度偏差可计算出机器人的横向和纵向速度,限制其旋转速度。由式(3)得到机器人4个轮子的速度,并发送到给机器人底盘,驱动机器人运动,通过不断向前迭代,最终使机器人运动到最终目标点。
2. 实验结果与分析
为验证本文提出融合算法的有效性,在Ubuntu18.04环境下,基于机器人操作系统(robot operating system,ROS)的移动机器人平台XIAO–MINI,进行室内导航实验。该平台是科大讯飞(苏州)科技有限公司提供的一款以麦克纳姆轮底盘构建的四轮全向移动机器人。
2.1 测试准备
将机器人放在搭建好的室内环境中,如图3。启动机器人进行建图,通过PC端的Ubuntu系统控制机器人缓慢移动,顶端的激光雷达扫描周围环境信息,采用ROS功能包中的Gmapping算法完成地图构建,利用ROS中RVIZ可视化工具观察地图建立的过程,直到所需环境地图建立完成。
2.2 自主导航测试
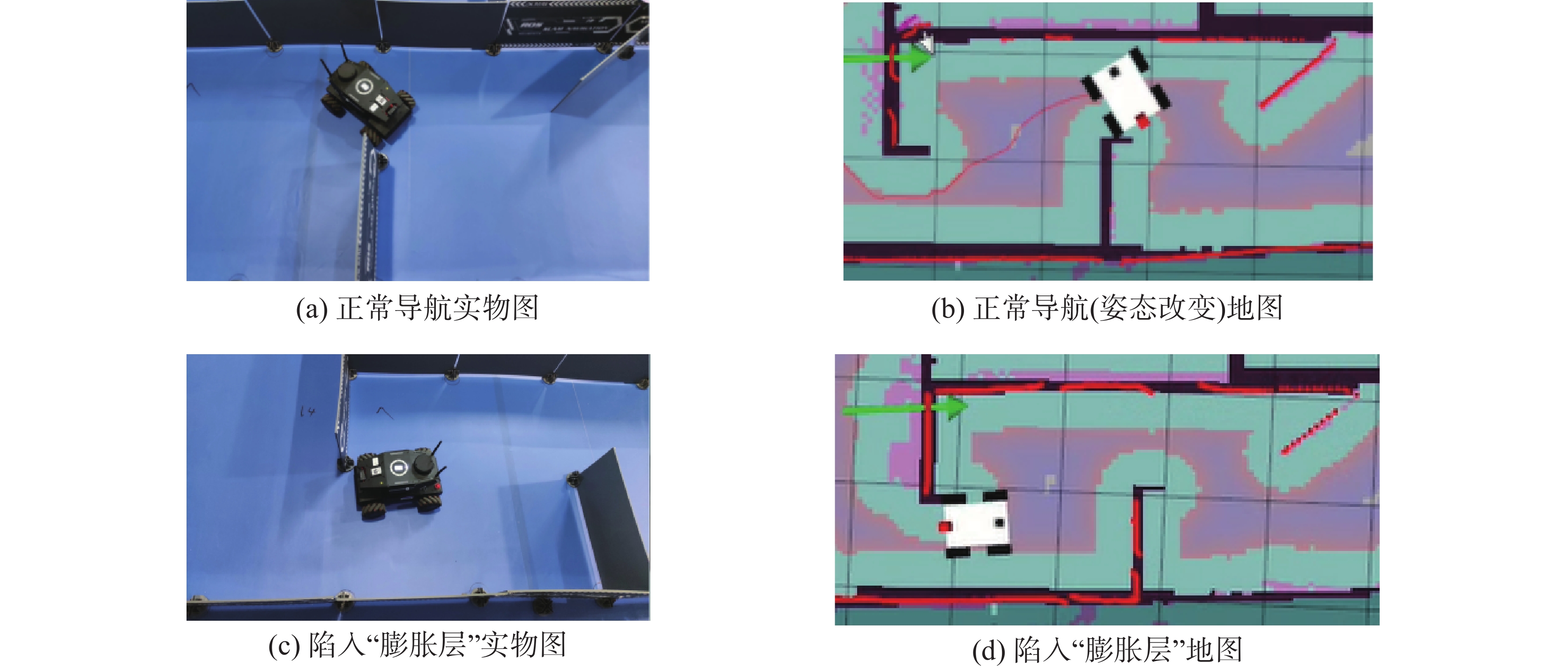
将预先建立的地图加载到导航节点中,运行导航功能包,初始化机器人的位姿,通过RVIZ可见地图中的机器人,这和机器人在真实环境中的位姿是一一对应的;发布任意在地图中的坐标点作为机器人本次运动的目标点,控制算法就会分别生成一条全局路径和局部路径,机器人开始运动。设置机器人的初始位姿为(−3.166,0.504,0,0,0,0,1.0),目标点位姿为(−0.134,0.167,0,0,0,0,1.0);机器人最大速度为0.5 m/s,最大角速度为2.75 rad/s,最大加速度为1.0 m/s2。在相同全局路径规划算法的前提下,使用TEB算法与本文提出的融合算法分别控制XIAO–MINI机器人进行25次自主导航实验,2种算法导航过程如图4,5。比较图4,5可看出:使用TEB算法导航,机器人出现姿态变化、碰撞障碍物及进入“膨胀层”无法继续导航的情况;本文算法在导航规划过程中能够更好地接近全局路径,机器人在运动过程中位姿没有发生较大的改变。
机器人在2种局部路径规划算法控制下的导航实验结果如表1。为降低实验偶然性,导航时间及导航成功率均为25次实验结果的平均值。
表 1 2种局部路径规划算法的导航时间和成功率Table 1. Navigation time and success rate of two local path planning algorithms算法 无障碍物 有障碍物 时间/s 导航成功率/% 时间减少比/% 时间/s 导航成功率/% 时间减少比/% TEB 19.2521 100 26.133 4 92 本文 13.3682 100 30.56 15.640 1 96 40.15 从表1可看出:对于由麦克纳姆轮底盘构建的机器人移动平台,与TEB算法比较,采用本文算法控制可有效减少机器人导航时间,在无障碍物的环境中可节省30.56%的时间,在有障碍物的环境中可节省40.15%的时间;在无障碍物的环境中,2种算法都能够安全到达目标点;在有障碍物的环境中,2种算法的导航成功率均达90%以上,但本文算法较TEB算法高4%。这是因为使用本文融合算法的机器人移动平台可不改变自身姿态进行移动,避免了机器人在转弯时姿态的改变,可极大缩短导航时间,同时提升导航成功率。
3. 结 论
针对以麦克纳姆轮为底盘的移动机器人在导航时跟随全局路径性较差、转弯半径过大以及无法在复杂狭小环境下避障的问题,提出一种融合Dijkstra和PID控制算法为核心的局部路径规划算法,采用TEB算法与本文提出的融合路径规划算法控制四轮全向移动机器人进行室内导航比较实验。结果显示:机器人可成功从设定的起点到达终点,在无障碍物的环境下,融合路径规划算法的平均导航时间为13.368 2 s,与TEB算法相比导航时间减少约30.56%;在有障碍的环境中,融合路径规划算法的导航成功率比TEB算法高4%。提出的融合路径规划算法可满足室内移动机器人的导航需求,规划的局部路径更加贴近全局路径,实现了导航效率和安全性的优化。由于本文实验是在室内搭建的环境中测试的,机器人在复杂室内环境下的鲁棒性仍存在不足,后续需进一步优化路径规划算法,在实际环境中部署动态障碍物,以适应更复杂的室内环境。
-
表 1 2种局部路径规划算法的导航时间和成功率
Table 1 Navigation time and success rate of two local path planning algorithms
算法 无障碍物 有障碍物 时间/s 导航成功率/% 时间减少比/% 时间/s 导航成功率/% 时间减少比/% TEB 19.2521 100 26.133 4 92 本文 13.3682 100 30.56 15.640 1 96 40.15 -
[1] ZHANG L,LI Y. Mobile robot path planning algorithm based on improved A star[J]. Journal of Physics: Conference Series, 2021, 1848(1):012013. doi: 10.1088/1742-6596/1848/1/012013
[2] 李全勇,李波,张瑞,等. 基于改进Dijkstra算法的AGV路径规划研究[J]. 机械工程与自动化, 2021(1):23−25,28. doi: 10.3969/j.issn.1672-6413.2021.01.008 [3] YANG H,QI J,MIAO Y,et al. A new robot navigation algorithm based on a double-layer ant algorithm and trajectory optimization[J]. IEEE Transactions on Industrial Electronics, 2019, 66(11):8557−8566. doi: 10.1109/TIE.2018.2886798
[4] WANG L,XU H X,CAO J H,et al. Improved ant colony-genetic algorithm for information transmission path optimization in remanufacturing service system[J]. Chinese Journal of Mechanical Engineering, 2018, 31(6):106−117.
[5] ZHANG S,LIAO Z H,WU Y,et al. Mobile robot path planning compares wavefront and A* algorithms[J]. Journal of Physics:Conference Series, 2021, 1948(1):012046. doi: 10.1088/1742-6596/1948/1/012046
[6] 彭求志,田丽,吴道华,等. 基于混合算法的机器人路径规划[J]. 安徽大学学报(自然科学版), 2021, 45(5):77−83. [7] 赵卫东,唐顾杰. 基于改进JPS与三次B样条插值的路径规划算法[J]. 安徽工业大学学报(自然科学版), 2022, 39(2):189−195. [8] CHANG L,SHAN L,JIANG C,et al. Reinforcement based mobile robot path planning with improved dynamic window approach in unknown environment[J]. Autonomous Robots, 2021, 45(1):51−76. doi: 10.1007/s10514-020-09947-4
[9] FOX D,BURGARD W. The dynamic window approach to collision avoidance[J]. IEEE Robotics & Automation Magazine, 1997, 4(1):23−33.
[10] 徐保来,管贻生,苏泽荣,等. 改进动态窗口法的阿克曼移动机器人局部路径规划器[J]. 机电工程技术, 2016, 45(9):21−26. doi: 10.3969/j.issn.1009-9492.2016.09.005 [11] ZHANG J H,FENG Q,ZHAO A D,et al. Local path planning of mobile robot based on self-adaptive dynamic window approach[J]. Journal of Physics:Conference Series, 2021, 1905(1):012019. doi: 10.1088/1742-6596/1905/1/012019
[12] 郑凯林,韩宝玲,王新达. 基于改进TEB算法的阿克曼机器人运动规划系统[J]. 科学技术与工程, 2020, 20(10):3997−4003. doi: 10.3969/j.issn.1671-1815.2020.10.030 [13] 王琦,王丽. 带麦克纳姆轮寻光追踪小车的设计与实现[J]. 工程机械, 2021, 52(3):1−7,137. doi: 10.3969/j.issn.1000-1212.2021.03.002 [14] 张禹,朱光召. 基于麦克纳姆轮的全方位移动平台技术研究[J]. 现代制造技术与装备, 2017(2):14−16. doi: 10.3969/j.issn.1673-5587.2017.02.009 [15] LIU G M,LI C H,GAO T T,et al. Double BP Q-learning algorithm for local path planning of mobile robot[J]. Journal of Computer and Communications, 2021, 9(6):138−157. doi: 10.4236/jcc.2021.96008
[16] 张美玉,简琤峰,侯向辉,等. Dijkstra算法在多约束农产品配送最优路径中的研究应用[J]. 浙江工业大学学报, 2012, 40(3):321−325,330. -
期刊类型引用(11)
1. 郭建,杨朋,曾志豪,黄颖驹,王家淳. 融合改进Dijkstra算法和动态窗口法的移动机器人路径规划. 组合机床与自动化加工技术. 2024(03): 36-40 .  百度学术
百度学术
2. 袁新亚,戴娟,孙胜强,刘经纬. 融合A~*和DWA算法的移动机器人路径规划方法. 电子测量技术. 2024(04): 95-103 .  百度学术
百度学术
3. 朱明超,吕镇炯,邓民翰,苏秉华,郑裕源,陈骏白. 基于多传感器融合的自主导航ROS智能机器人. 自动化应用. 2024(13): 1-4 .  百度学术
百度学术
4. 张明月,王军. 基于改进双向快速扩展随机树算法的智能汽车路径规划研究. 汽车工程师. 2024(10): 31-36 .  百度学术
百度学术
5. 王鹏杰,李丹,付金岗,龚旭,赵文杰. 融合改进RRT和TEB算法的移动焊接机器人路径规划. 安徽工业大学学报(自然科学版). 2024(06): 620-626 .  百度学术
百度学术
6. 侯艳丽,马震. 基于深度优先搜索的分层网络最短路径算法. 无线电通信技术. 2023(04): 684-688 .  百度学术
百度学术
7. 赵卫东,周大昌. 基于A~*与三阶贝塞尔曲线的融合改进路径规划算法. 安徽工业大学学报(自然科学版). 2023(03): 333-338 .  百度学术
百度学术
8. 李纪鑫,吴宗卓,赫磊,任高明. 多机器人协同的SLAM算法研究. 自动化与仪器仪表. 2023(09): 205-209 .  百度学术
百度学术
9. 闫振. 移动机器人路径规划算法分析. 传感器世界. 2023(08): 1-8+20 .  百度学术
百度学术
10. 吴凡,张华,童以,刘苏杭. 多传感器融合的温室机器人自主导航系统设计. 安徽科技学院学报. 2023(06): 96-102 .  百度学术
百度学术
11. 姜文军,吕东波,陈正隆,李晓贞. 手术机器人万向关节组的正逆运动学分析. 安徽科技学院学报. 2023(06): 103-110 .  百度学术
百度学术
其他类型引用(12)



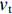
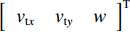



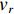
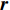
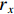
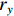
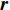

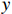
 下载:
下载: